با روش های میانبر محاسبات سریع ذهنی قدرت ذهن خود را صدبرابرکنید

بخشی از آموزش ویدئویی فارسی مجموعه تقویت حافظه کوانتومی کوثرپرداز ، آموزش تکنیک های میان بر محاسبات سریع ذهنی است. تکنیک هایی که اگر به آنها مسلط شوید می توانید بخش زیادی از محاسبات آزمون ها و امتحان ها و همچنین حساب و کتاب های روزانه زندگی خود را با سرعتی باورنکردنی ،به صورت ذهنی و بدون نیاز به ماشین حساب و چرتکه و ابزارهای کمکی انجام دهید. با این قدرت اعجاب آور شما در همه جا کلاس و مدرسه و بازار ، اطرافیان خود را به حیرت خواهید انداخت و از همه مهم تر قدرت ذهن خود را به جای هدر دادن روی انجام محاسبات وقت گیر ، روی موضوعات کلیدی تر متمرکز خواهید نمود. در اینجا بخشی از این محاسبات میانبر را با هم مرور می کنیم. بقیه این محاسبات را می توانید در ادامه مطلب همین پست دنبال کنید.

******

ترفند هایی ساده برای محاسبات سریع ذهنی

راه حل ضرب ذهنی اعداد دورقمی زیر ۲۰ کشف شد

با این ترفند ، قادر خواهید بود هر دو عددی ، از 11 تا 19 را بدون استفاده از ماشین حساب، بسرعت در ذهن خود ضرب کنید. ( البته با فرض اینکه جدول ضرب رو خوب بلد باشید ) در این جا به طور مثال 16 × 19 را آزمایش می کنیم.

عملیات : عدد بزرگتر را با یکان عدد کوچکتر جمع کنید . ( یعنی 25 = 6 + 19 ) و در جلوی حاصلجمع صفری قرار دهید (250 ) . سپس یکان دو عد را در هم ضرب کنید و با عدد قبلی جمع کنید . ( یعنی 54 = 6 × 9 و 304 = 54 + 250 ) جواب ما 304 است.

اگر این عمل را چند بار تکرار کنید به راحتی و در دو سه ثانیه می تونید ضرب های دورقمی زیر 20 رو حل کنید.

یه روش دیگه هم هست ... یکان ها رو با هم جمع کنید و ضربدر 10 کنید و با ضرب یکان ها جمع کنید و در نهایت بعلاوه ی 100 کنید !!

اینطوری برای اعداد بین 20 و 30 یا بین 30 و 40 یا .... هم میشه تعمیم داد !
مثلا برای 20 تا 30 ... یکان ها را با هم جمع کنید و ضربدر 20 کنید و با ضرب یکان ها جمع کنید و در نهایت بعلاوه ی 400 کنید ! (البته ضربدر 20 کردن یکم سخت تر میشه .. مخصوصا بیشتر از 30 ها ... )

گاهی اوقات اگر دقت کنید که چه انجام می دهید، الگوریتم های ضربی میانبر های ضربی زیبایی را به شما معرفی می کنند.

از شما می خواهیم که ضرب های مختلفی را با اعداد 21 و 31 و 41 و 51 و ... انجام دهید. بااین کار شما به زودی به سمت ِ میانبر های زیبای ضربی روان خواهید شد.

چگونگی ضرب کردن با بیست و یک : عدد اصلی را دو برابر کنید و حاصل را در 10 ضرب کنید . سرانجام عدد اصلی را به آن بیافزایید.

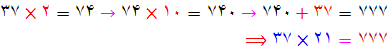
چگونگی ضرب کردن با سی و یک :عدد اصلی را سه برابر کنید و حاصل را در 10 ضرب کنید . سرانجام عدد اصلی را به آن بیافزایید

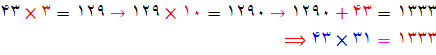
چگونگی ضرب کردن با  :چهل و یک  عدد اصلی را چهار برابر کنید و حاصل را در 10 ضرب کنید . سرانجام عدد اصلی را به آن بیافزایید.

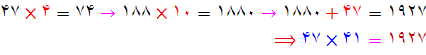
جمع کردن دو عدد از چپ به راست خیلی سریع تر صورت می گیرد. به جمع زیر دقت کنید:

این هم نحوه جمع کردن از چپ به راست برای اعداد سه رقمی :

برای تفریق دو عدد هم می توان از شیوه تفریق چپ به راست استفاده کرد:

با استفاده از مکمل اعداد می توان تفریق ذهنی اعداد سنگین تر را نیز سریع انجام داد. به تفریق زیر دقت کنید. در آن از مکمل اعداد استفاده شده است.

از شیوه جادویی محاسبه چپ به راست که دقیقا خلاف روش محاسبه راست به چپی است که در دوره دبستان به ما یاد داده اند می توانیم جمع و تفریق های سنگین را نیز به راحتی با روش ذهنی حساب کنیم:

برای ضرب دو عدد نیز می توان از شیوه محاسبه چپ به راست استفاده کرد.

ویا

و یا برای ضرب دو عدد 88×97:

تکنیکی ساده برای توان دو رساندن اعداد دو رقمی - رقم یکان را از عدد مذکور جمع و تفریق می کنیم و بعد دو عدد حاصل را در هم ضرب و با توان دو رقم یکان مربوطه جمع می کنیم. در زیر برای عدد سیزده به توان دو این کار را انجام داده ایم:

برای توان دو رساندن اعداد دو رقمی دیگر مانند 43 و 52 به شکل زیر عمل می کنیم:

برای رسیدن به فرمول محاسبه از اتحاد ساده زیر استفاده کردیم:

.

بنابراین با کمک فرمول فوق می توانیم به راحتی توان دو هر عدد دو رقمی دلخواه را به صورت ذهنی و سریع حساب کنیم. کافی است طبق مراحل زیر عمل کنیم:

مثال های دیگر در ادامه مطلب آورده شده است.

11

مثال های بیشتر برای توان دو رساندن اعداد دورقمی به صورت ذهنی و سریع:

e.g 2]
 
17²=(17+3) (17-3)+3²

      = 20×14+9

      = 280+9
      = 289



e.g 3]
   
46²=(46+4) (46-4)+4²

      = 50×42+16

      = 2100+16
      =2116



e.g 4]
   
52²=(52+2) (52-2)+2²

       =54×50+4

       =2700+4
       =2704

just follow the step and try to do all the calculation in your head.


e.g 5]

67²= (67+3) (67-3)+3²

      = 70×64+9
      = 4489





e.g 6]
 

59²= (59+1) (59-1)+1²

      = 58×60+1
      = 3481




e.g 7]

86²=(86+4) (86-4)+4²

       = 90×82+16
       = 7396


e.g 8]

98²=(98+2) (98-2)+2²

      = 100×96+4
      = 9604

 Here we are done with our squaring trick, the squaring problem cannot be much tougher then what i  had shown you above. So from now make your own example and keep on practicing.

This squaring trick Remind me of multiplication trick of multiplying two digit number like 14×12.


e.g 1]
  14

×12

14+2=16  ....................In this trick we add 2, second digit of opposite figure.

160  ............................. then add a zero to 16 to get 160

160+8 ......................... We get 8 by multiplying 2×4, the second digit of our both the numbers. 

168 Our answer        Add 8+160 and we are done.


e.g 2]  16×13

           =16+3

           =190  ................add zero in end of 16+3

           =208  ................multiply 6×3 and add it hear with 190